Deontic logic is the field of logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. Typically, a deontic logic uses OA to mean it is obligatory that A, (or it ought to be (the case) that A), and PA to mean it is permitted (or permissible) that A. The term deontic is derived from the ancient Greek déon, meaning, roughly, that which is binding or proper.

History
Philosophers from the Indian Mimamsa school to those of Ancient Greece have remarked on the formal logical relations of deontic concepts In his Elementa juris naturalis, Leibniz notes the logical relations between the licitum, illicitum, debitum, and indifferens are equivalent to those between the possible, impossible, necessarium, and contingens respectively.
Pre-History of Deontic Logic
Ernst Mally, a pupil of Alexius Meinong, was the first to propose a formal system of deontic logic in his Grundgesetze des Sollens and he founded it on the syntax of Whitehead's and Russell's propositional calculus. Mally's deontic vocabulary consisted of the logical constants U and ∩, unary connective !, and binary connectives f and ∞. * Mally read !A as "A ought to be the case". * He read A f B as "A requires B" . * He read A ∞ B as "A and B require each other." * He read U as "the unconditionally obligatory" . * He read ∩ as "the unconditionally forbidden". Mally defined f, ∞, and ∩ as follows:
Def. f. A f B = A → !B Def. ∞. A ∞ B = (A f B) & (B f A) Def. ∩. ∩ = ¬U Mally proposed five informal principles:
(i) If A requires B and if B then C, then A requires C. (ii) If A requires B and if A requires C, then A requires B and C. (iii) A requires B if and only if it is obligatory that if A then B. (iv) The unconditionally obligatory is obligatory. (v) The unconditionally obligatory does not require its own negation. He formalized these principles and took them as his axioms:
I. ((A f B) & (B → C)) → (A f C) II. ((A f B) & (A f C)) → (A f (B & C)) III. (A f B) ↔ !(A → B) IV. ∃U !U V. ¬(U f ∩) From these axioms Mally deduced 35 theorems, many of which he rightly considered strange. Karl Menger showed that !A ↔ A is a theorem and thus that the introduction of the ! sign is irrelevant and that A ought to be the case iff A is the case. After Menger, philosophers no longer considered Mally's system viable. Gert Lokhorst lists Mally's 35 theorems and gives a proof for Menger's theorem at the Stanford Encyclopedia of Philosophy under Mally's Deontic Logic. The first plausible system of deontic logic was proposed by G. H. von Wright in his paper Deontic Logic in the philosophical journal Mind in 1951. (Von Wright was also the first to use the term "deontic" in English to refer to this kind of logic although Mally published the German paper Deontik in 1926.) Since the publication of von Wright's seminal paper, many philosophers and computer scientists have investigated and developed systems of deontic logic. Nevertheless, to this day deontic logic remains one of the most controversial and least agreed-upon areas of logic. G. H. von Wright did not base his 1951 deontic logic on the syntax of the propositional calculus as Mally had done, but was instead influenced by alethic modal logics, which Mally had not benefited from. In 1964, von Wright published A New System of Deontic Logic, which was a return to the syntax of the propositional calculus and thus a significantly return to Mally's system. (For more on von Wright's departure from and return to the syntax of the propositional calculus, see Deontic Logic: A Personal View and A New System of Deontic Logic, both by Georg Henrik von Wright.) G. H. von Wright's adoption of the modal logic of possibility and necessity for the purposes of normative reasoning was a return to Leibniz.

Mally's First Deontic Logic and von Wright's First Plausible Deontic Logic
In von Wright's first system, obligatoriness and permissibility were treated as features of acts. It was found not much later that a deontic logic of propositions could be given a simple and elegant Kripke-style semantics, and von Wright himself joined this movement. The deontic logic so specified came to be known as "standard deontic logic," often referred to as SDL, KD, or simply D. It can be axiomatized by adding the following axioms to a standard axiomatization of classical propositional logic:


In English, these axioms say, respectively:
FA, meaning it is forbidden that A, can be defined (equivalently) as or .
The propositional system D can be extended to include quantifiers in a relatively straightforward way.

If it ought to be that A implies B, then if it ought to be that A, it ought to be that B;
If it ought to be that A, then it is permissible that A. Standard deontic logic
An important problem of deontic logic is that of how to properly represent conditional obligations, e.g. If you smoke (s), then you ought to use an ashtray (a). It is not clear that either of the following representations is adequate:


Under the first representation it is vacuously true that if you commit a forbidden act, then you ought to commit any other act, regardless of whether that second act was obligatory, permitted or forbidden (Von Wright 1956, cited in Aqvist 1994). Under the second representation, we are vulnerable to the gentle murder paradox, where the plausible statements if you murder, you ought to murder gently, you do commit murder and to murder gently you must murder imply the less plausible statement: you ought to murder.
Some deontic logicians have responded to this problem by developing dyadic deontic logics, which contain a binary deontic operators:
means it is obligatory that A, given B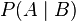
means it is permissible that A, given B.
(The notation is modeled on that used to represent conditional probability.) Dyadic deontic logic escapes some of the problems of standard (unary) deontic logic, but it is subject to some problems of its own.

Dyadic deontic logic
Many other varieties of deontic logic have been developed, including non-monotonic deontic logics, paraconsistent deontic logics, and dynamic deontic logics.

Other variations
Deontic logic faces Jørgensen's Dilemma. Norms cannot be true or false, but truth and truth values seem essential to logic. There are two possible answers:

Deontic logic handles norm propositions, not norms;
There might be alternative concepts to truth, e.g. validity or success, as it is defined in speech act theory. Jørgensen's Dilemma

Modal logic
Imperative logic
Norm (philosophy)