The Coriolis effect is the apparent deflection of moving objects from a straight path when they are viewed from a rotating frame of reference. The effect is named after Gaspard-Gustave Coriolis, a French scientist who described it in 1835, though the mathematics appeared in the tidal equations of Pierre-Simon Laplace in 1778. One of the most notable examples is the deflection of winds moving along the surface of the Earth to the right of the direction of travel in the Northern hemisphere and to the left of the direction of travel in the Southern hemisphere. This effect is caused by the rotation of the Earth and is responsible for the direction of the rotation of large cyclones: winds around the center of a cyclone rotate counterclockwise on the northern hemisphere and clockwise on the southern hemisphere.
The Coriolis effect is caused by the Coriolis force, which appears in the equation of motion in a rotating frame of reference. Sometimes this force is called a fictitious force (or pseudo force), because it does not appear when the motion is expressed in an inertial frame of reference. In such a frame, the motion is explained by the real impressed forces, together with inertia. In a rotating frame, the Coriolis and centrifugal forces are needed in the equation to correctly describe the motion.
Contrary to popular belief, the Coriolis effect is not the determining factor in the rotation of water in toilets or bathtubs (see the Draining bathtubs and toilets section below).

Formula
The Coriolis effect exists only when using a rotating reference frame. It is mathematically deduced from the law of inertia. Hence it does not correspond to any actual acceleration or force, but only the appearance thereof from the point of view of a rotating system.
The Coriolis effect exhibited by a moving object can be interpreted as being the sum of the effects of two different causes of equal magnitude.
The first cause is the change of the velocity of an object in time. The same velocity (in an inertial frame of reference where the normal laws of physics apply) will be seen as different velocities at different times in a rotating frame of reference. The apparent acceleration is proportional to the angular velocity of the reference frame (the rate at which the coordinate axes changes direction), and to the velocity of the object. This gives a term . The minus sign arises from the traditional definition of the cross product (right hand rule), and from the sign convention for angular velocity vectors.
The second cause is change of velocity in space. Different points in a rotating frame of reference have different velocities (as seen from an inertial frame of reference). In order for an object to move in a straight line it must therefore be accelerated so that its velocity changes from point to point by the same amount as the velocities of the frame of reference. The effect is proportional to the angular velocity (which determines the relative speed of two different points in the rotating frame of reference), and the velocity of the object perpendicular to the axis of rotation (which determines how quickly it moves between those points). This also gives a term .

Causes

The Coriolis effect is not a result of the curvature of the Earth, only of its rotation. (However, the value of the Coriolis parameter, 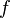, does vary with latitude, and that dependence is due to the Earth's shape.)
The fact that ballistic missiles and satellites appear to follow curved paths when plotted on common world maps is mainly due to the fact that the earth is spherical and the shortest distance between two points on the earth's surface (called a great circle) is usually not a straight line on those maps. Every two-dimensional (flat) map necessarily distorts the earth's curved (three-dimensional) surface in some way. Typically (as in the commonly used Mercator projection, for example), this distortion increases with proximity to the poles. In the northern hemisphere for example, a ballistic missile fired toward a distant target using the shortest possible route (a great circle) will appear on such maps to follow a path north of the straight line from target to destination, and then curve back toward the equator. This occurs because the latitudes, which are projected as straight horizontal lines on most world maps, are in fact circles on the surface of a sphere, which get smaller as they get closer to the pole. Being simply a consequence of the sphericity of the Earth, this would be true even if the Earth didn't rotate. The Coriolis effect is of course also present, but its effect on the plotted path is much smaller.
The Coriolis force should not be confused with the centrifugal force given by . A rotating frame of reference will always cause a centrifugal force no matter what the object is doing (unless that body is particle-like and lies on the axis of rotation), whereas the Coriolis force requires the object to be in motion relative to the rotating frame with a velocity that is not parallel to the rotation axis. Because the centrifugal force always exists, it can be easy to confuse the two, making simple explanations of the effect of Coriolis in isolation difficult. In particular, when is tangential to a circle centered on and perpendicular to the axis of rotation, the Coriolis force is parallel to the centrifugal force. It is then possible to construct a rotating reference frame of a different rotational speed, where is zero and there is no Coriolis force What the Coriolis effect is not
To demonstrate the Coriolis effect, a parabolic turntable can be used. On a flat turntable the centrifugal force, which always acts outwards from the rotation axis, would force co-rotating objects off the edge. But if the surface of the turntable has the correct parabolic bowl shape and is rotated at the correct rate, then the component of gravity tangential to the bowl surface will exactly equal the centripetal force necessary to keep the water rotating at its velocity and radius of curvature. This allows the Coriolis force to be displayed in isolation. When a container of fluid is rotating on a turntable, the surface of the fluid naturally assumes the correct parabolic shape. This fact may be exploited to make a parabolic turntable by using a fluid that sets after several hours, such as a synthetic resin.
Discs cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing effects of Coriolis on dynamic phenomena to show themselves. To get a view of the motions as seen from the reference frame rotating with the turntable, a video camera is attached to the turntable so as to co-rotate with the turntable. Because this reference frame rotates several times a minute, rather than only once a day like the Earth, the Coriolis acceleration produced is many times larger, and so easier to observe on small time and spatial scales, than is the Coriolis acceleration caused by the rotation of the Earth.
In a manner of speaking, the Earth is analogous such a turntable. The rotation has caused the planet to settle on a spheroid shape such that the normal force, the gravitational force, and the centrifugal force exactly balance each other on a "horizontal" surface. (See equatorial bulge.)
The Coriolis effect caused by the rotation of the Earth can be seen indirectly through the motion of a Foucault pendulum.

Visualization of the Coriolis effect
A misconception in popular culture is that the Coriolis effect determines the direction in which bathtubs or toilets drain, such that water always drains in one direction in the Northern Hemisphere, and in the other direction in the Southern Hemisphere. This urban legend has been perpetuated by several television programs, including an episode of The Simpsons and The X-Files.
When the water is being drawn towards the drain, the radius with which it is spinning around it decreases, so its rate of rotation increases from the low background level to a noticeable spin in order to conserve its angular momentum (the same effect as ice skaters bringing their arms in to cause them to spin faster). As shown by Ascher Shapiro in a 1961 educational video (Vorticity, Part 1), this effect can indeed reveal the influence of the Coriolis force on drain direction, but only under carefully controlled laboratory conditions. In a large, circular, symmetrical container (ideally over 1m in diameter and conical), still water (whose motion is so little that over the course of a day, displacements are small compared to the size of the container) escaping through a very small hole, will drain in a cyclonic fashion: counterclockwise in the Northern hemisphere and clockwise in the Southern hemisphere—the same direction as the Earth rotates with respect to the corresponding pole.

Draining bathtubs and toilets
Perhaps the most important instance of the Coriolis effect is in the large-scale dynamics of the oceans and the atmosphere. In meteorology, it is convenient to use a rotating frame of reference where the Earth is stationary. The fictitious centrifugal and Coriolis forces must then be introduced. The former, however, is cancelled by the non-spherical shape of the earth (see the turntable analogy above). Hence the Coriolis force is the only fictitious force to have a significant impact on calculations.

Coriolis in meteorology
If a low-pressure area forms in the atmosphere, air will tend to flow in towards it, but will be deflected perpendicular to its velocity by the Coriolis acceleration. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow.
The force balance is largely between the pressure gradient force acting towards the low-pressure area and the Coriolis force acting away from the center of the low pressure. To get some grip on the size of the effect, consider a high-pressure area at 1020 millibars at a distance of 1000 km from a low at 980 millibars. The pressure gradient is then 0.004 N/m Cyclones cannot form on the equator, because in the equatorial region the coriolis parameter is small, and exactly zero on the equator.

Flow around a low-pressure area
An air or water mass moving with speed subject only to the Coriolis force travels in a circular trajectory called an 'inertial circle'. Since the force is directed at right angles to the motion of the particle, it will move with a constant speed, and perform a complete circle with frequency f. The magnitude of the Coriolis force also determines the radius of this circle: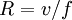
.
On the Earth, a typical mid-latitude value for f is 10; hence for a typical atmospheric speed of 10 m/s the radius is 100 km, with a period of about 14 hours. In the ocean, where a typical speed is closer to 10 cm/s, the radius of an inertial circle is 1 km. These inertial circles are clockwise in the northern hemisphere (where trajectories are bent to the right) and anti-clockwise in the southern hemisphere.
If the rotating system is a parabolic turntable, then f is constant and the trajectories are exact circles. On a rotating planet, f varies with latitude and the paths of particles do not form exact circles. Since the parameter f varies as the sine of the latitude, the radius of the oscillations associated with a given speed are smallest at the poles (latitude = ±90°), and increase toward the equator.

Inertial circles
Further information: Rossby number
The time, space and velocity scales are important in determining the importance of the Coriolis effect. Whether rotation is important in a system can be determined by its Rossby number, which is the ratio of the velocity, U, of a system to the product of the Coriolis parameter, f, and the length scale, L, of the motion:
.
A small Rossby number signifies a system which is strongly affected by rotation, and a large Rossby number signifies a system in which rotation is unimportant.
An atmospheric system moving at U = 10 m/s occupying a spatial distance of L = 1000 km, has a Rossby number of approximately 0.1. A man playing catch may throw the ball at U = 30 m/s in a garden of length L = 50 m. The Rossby number in this case would be about = 6000. Needless to say, one does not worry about which hemisphere one is in when playing catch in the garden. However, an unguided missile obeys exactly the same physics as a baseball, but may travel far enough and be in the air long enough to notice the effect of Coriolis. Long-range shells in the Northern Hemisphere landed close to, but to the right of, where they were aimed until this was noted. (Those fired in the southern hemisphere landed to the left.)
The Rossby number can also tell us about the bathtub. If the length scale of the tub is about L=1m, and the water moves towards the drain at about 60cm/s, then the Rossby number is about 6 000. Thus, the bathtub is, in terms of scales, much like a game of catch, and rotation is likely to be unimportant.

Other terrestrial effects
The practical impact of the Coriolis effect is mostly caused by the horizontal acceleration component produced by horizontal motion.
There are other components of the Coriolis effect. Eastward-traveling objects will be deflected upwards (feel lighter), while westward-traveling objects will be deflected downwards (feel heavier). This is known as the Eötvös effect. This aspect of the Coriolis effect is greatest near the equator. The force produced by this effect is similar to the horizontal component, but the much larger vertical forces due to gravity and pressure mean that it is generally unimportant dynamically.
In addition, objects traveling upwards or downwards will be deflected to the west or east respectively. This effect is also the greatest near the equator. Since vertical movement is usually of limited extent and duration, the size of the effect is smaller and requires precise instruments to detect.

Other aspects of the Coriolis effect

Coriolis elsewhere
A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate and density of a fluid flowing through a tube. The operating principle, introduced in 1977 by Micro Motion Inc., involves inducing a vibration of the tube through which the fluid passes. The vibration, though it is not completely circular, provides the rotating reference frame which gives rise to the Coriolis effect. While specific methods vary according to the design of the flow meter, sensors monitor and analyze changes in frequency, phase shift, and amplitude of the vibrating flow tubes. The changes observed represent the mass flow rate and density of the fluid.

Coriolis flow meter
In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects will therefore be present and will cause the atoms to move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels.

Molecular physics
The Coriolis effects became important in external ballistics for calculating the trajectories of very long-range artillery shells. The most famous historical example was the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km. The Coriolis effect plays a role in almost all modern artillery trajectory calculations.

Insect flight